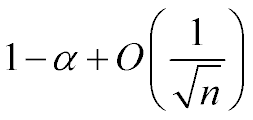Assume you have a sample of n observations Xn and you have some parameter estimator based on this sample (mean, variance, correlation, etc).
If you don't know the closed CI formula for a parameter (or just dont want to find it), the simple way to calculate this CI is bootstrapping.
In bootstrapping you resample your sample randomly WITH repetitions and calculate your parameter estimate.

After this process you have a sample of parameters - compute the required interval as follows:

why does this work? from the key idea:

But be careful: a bootstrap sample can only tell you things about the original sample, and won't give you any new information about the real population. It is simply a nonparametric method for constructing confidence intervals and similar. If you want to gain more information about the population, you have to gather more data from the population.
A great example is given in mathematica manual, where they find a confidence interval for sample skewness:
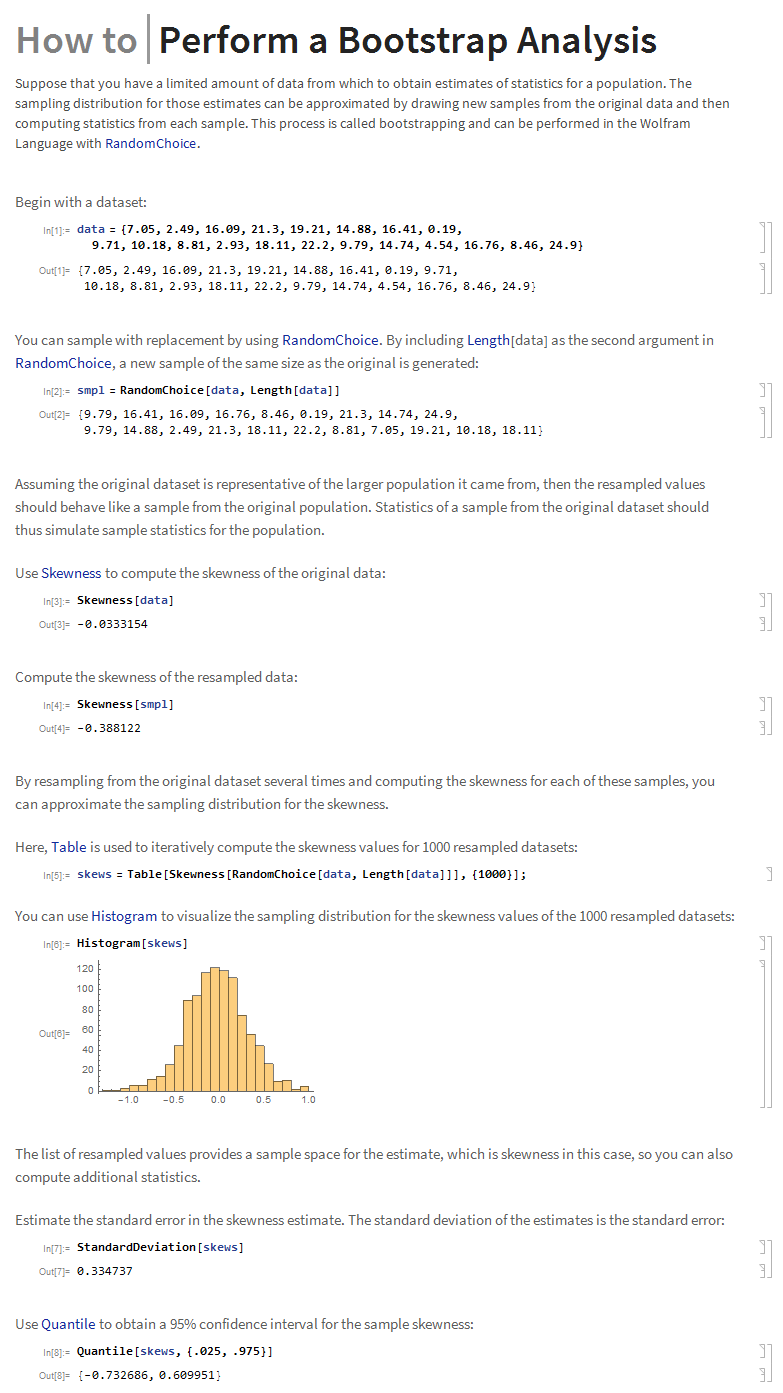
Mathematica manual above uses so called "Percentile bootstrap" or where we simply calculate the CI based on observed values, but not on their residuals. Both methods have their pros and cons.
Any bootstrap CI coverage has the following assymptotic behavior: