Markets sometimes lack direct price listings. Instead, historical records contain trades where sets of items were exchanged for other sets. Such records appear in barter economies, online game economies, item trading platforms, and decentralized markets.
The objective is to infer a fair, globally consistent exchange price between any two items using only past trades, even when some trades are incorrect, manipulated, or noisy.
In particular, consider Diablo 2 trading platform traderie.com where players can post listings of items they are willing to trade in a barter scheme.
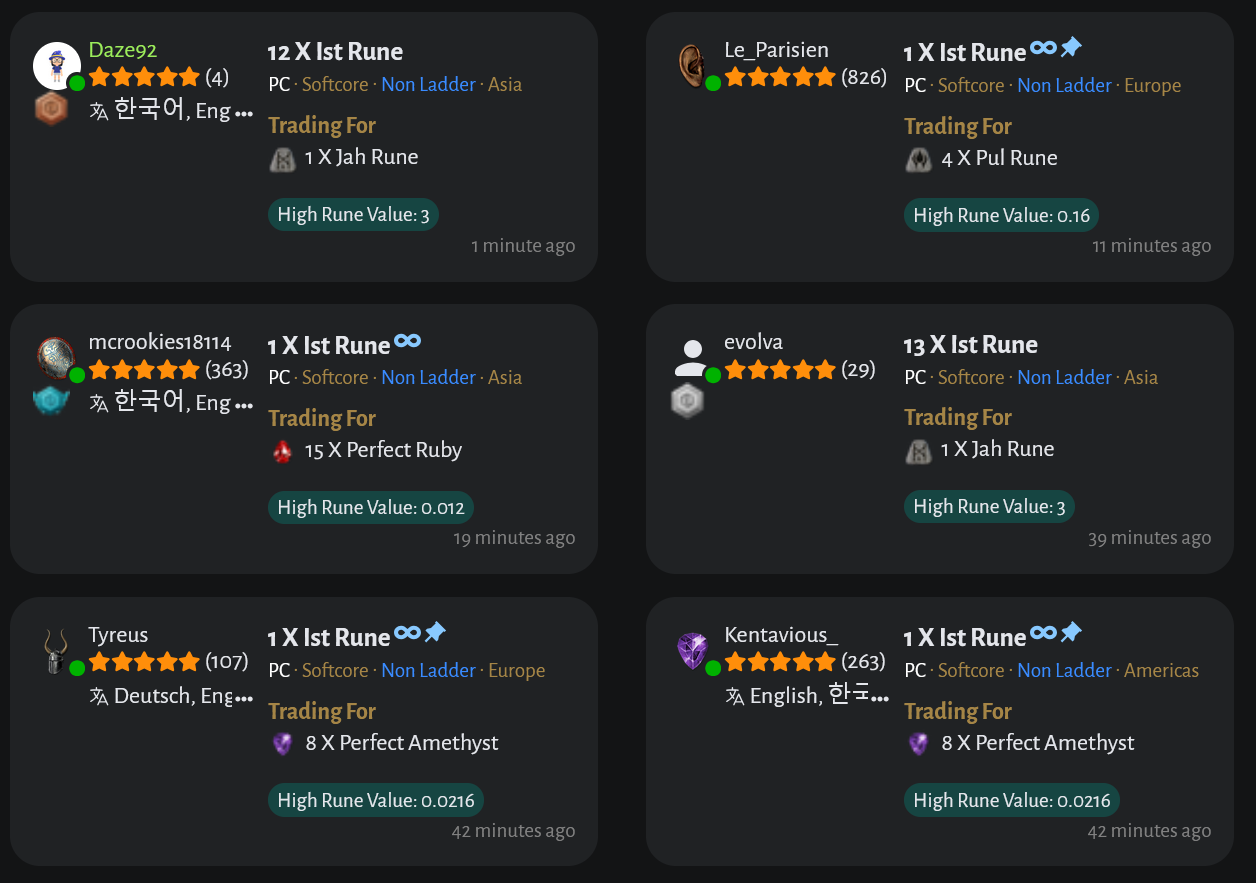
Representing Trades as Value Conservation
Assume that every item has an underlying latent value. Let:
- v[k] denote the unknown value of item
- Each trade exchanges set A for set B (A <~> B)
A rational trade approximately preserves value:
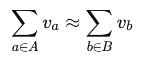
Each historical trade therefore provides a constraint linking item values.
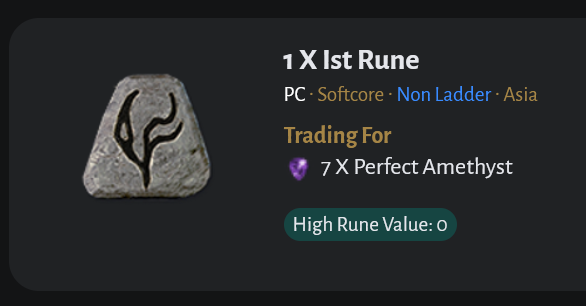
For example here a player who traded an Ist rune for a 7 perfect amethysts:
Converting Trades into Linear Equations
Each trade can be rewritten as:
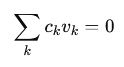
Where c[k]: number of item in set A minus number in set B
If all trades are stacked together, a linear system emerges:
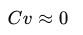
There C is the so called "trade matrix"
Multiplying all values by a constant produces identical trade relationships. The system therefore requires normalization.
One can take a "reference" item and set it's value to 1 to measure all other items in this value:
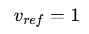
For the sake of numerical optimization I took v[Jah Rune] as 1 because it is considered the most expensive rune in the game. This stabilizes the numerical solver.
Once item values are estimated, fair exchange rates follow directly: p[i,j] = v[i]/v[j]
The Impact of Noise and Spurious Trade
Real trade data often contains mispriced transactions, trategic or irrational trade or market manipulation. A simple least-squares solution attempts to satisfy all trades equally, allowing large errors from bad data to distort results. Robust estimation is required.
A simple solution is to use the L1 norm optimization:
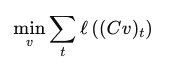
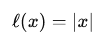
L1 norm optimization properties are well established for such a task
Optimization
The historical data from the past month (at the moment of writing) was downloaded and the analyzed with Wolfram Mathematica yielding the following values if measured in "Ist Rune" (mid value rune):
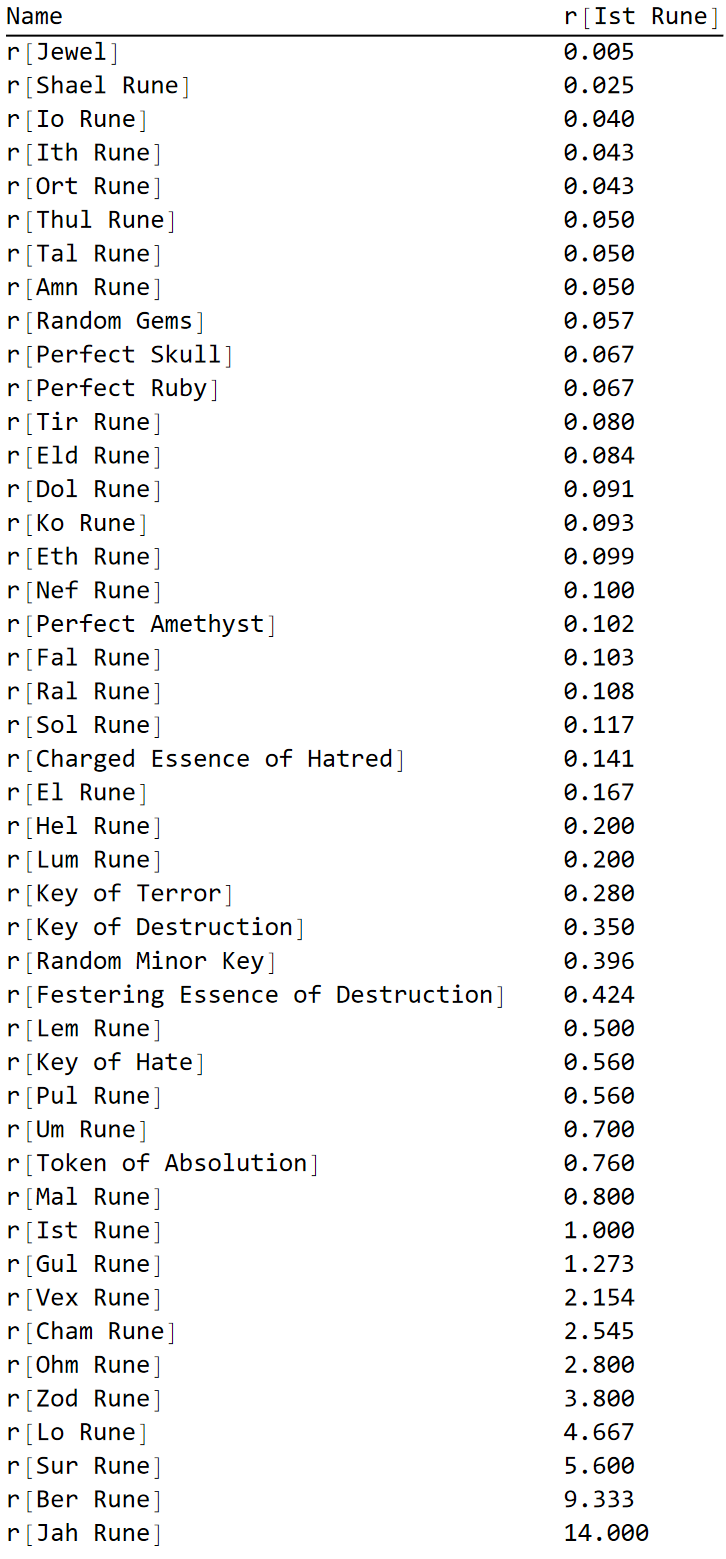
One can also take a peek at the market efficiency by analyzing the residuals of the fit model:
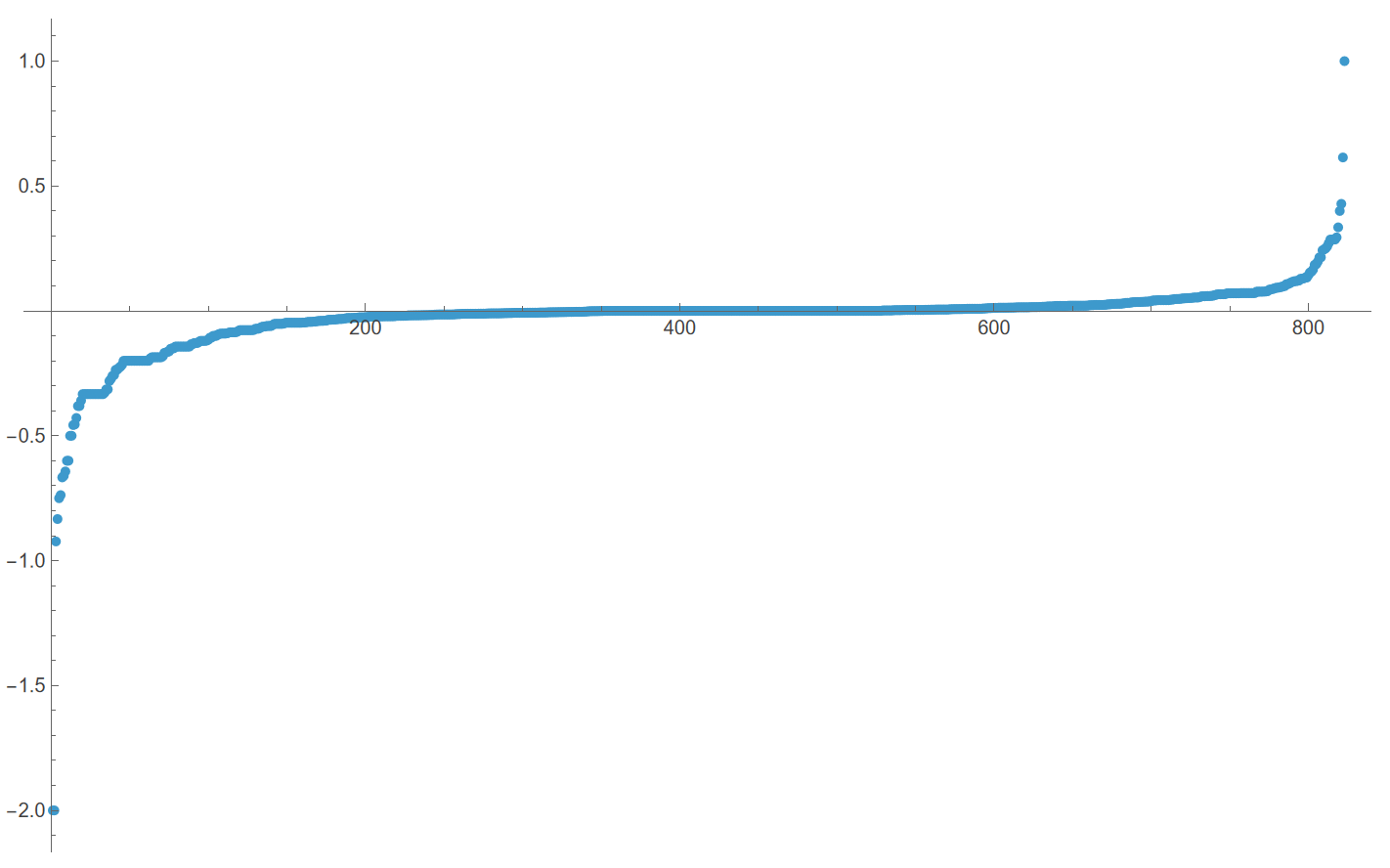
With top 5 most profitable trades being:
24 r[Lum Rune] for r[Sol Rune]
33 r[Lum Rune] for r[Ist Rune]
r[Jah Rune] for 40 r[Hel Rune]
17 r[Zod Rune] for 4 r[Jah Rune]
30 r[Ohm Rune] for 5 r[Jah Rune]
Great value, congratulations!
The top 5 unprofitable trades were:
11 r[Gul Rune] for 3 r[Jah Rune]
3 r[Lo Rune] for 3 r[Jah Rune]
7 r[Vex Rune] for 2 r[Jah Rune]
140 r[Sol Rune] for 2 r[Jah Rune]
140 r[Shael Rune] for r[Jah Rune]
Unlucky! But at least I hope you put them to good use.
Conclusion
Historical barter trades implicitly encode a system of value conservation equations. By modeling each item with an unknown latent value and solving a robust regression problem, consistent market exchange rates can be reconstructed. Robust loss functions and trade weighting are essential for maintaining stability in the presence of noisy or adversarial trade data.
This framework produces globally consistent prices, supports incomplete trade graphs, and scales efficiently with sparse numerical methods.