A Computational Essay to Strassen's Bases

1. What Strassen Did

In 1969, Volker Strassen discovered a way to multiply two 2×2 matrices with only 7 multiplications instead of 8. This lowered the exponent of matrix multiplication below 3 for the first time and opened the door to the entire field of fast matrix multiplication. The formulas - linear combinations of entries from the input matrices - look arbitrary and mysterious.

2. The Problem With the Formulas

Strassen's scheme is often presented as a set of clever tricks: seven products, then a reassembly into the correct result. But there is no canonical derivation. Every presentation either looks ad hoc, uses unexplained algebraic "guesses", or appeals to hindsight. Mathematicians agree the formulas work, but not how one should discover them from first principles.

Even the following set of resources does not provide a satisfactory explanation as to where exactly these formulas arrive from:

• Gideon Yuval, A simple proof of Strassen’s result
• Ann Q. Gates, Vladik Kreinovich, Strassen's Algorithm Made (Somewhat) More Natural: A Pedagogical Remark, 2001
• Jacob Minz, Derivation of Strassen's Algorithm for the multiplication of 2×2 matrices, 2015
• Christian Ikenmeyer, Vladimir Lysikov, Strassen's 2x2 matrix multiplication algorithm: A conceptual perspective, 2017
• Joshua A. Grochow, Christopher Moore, Designing Strassen’s Algorithm, 2017

All of these resources rely on "intuition", ad-hoc rationalization, hindsight bias or apriori knowledge. This does not suffice.

3. Monomials as 4×4 Matrices

Each product in the matrix multiplication expansion corresponds to a bilinear monomial, such as a11*b12. A systematic representation is to encode every possible product as a 4×4 matrix with a single 1 marking the position of the contributing pair (i,j). With this encoding, reasoning about subsets of monomials becomes combinatorial rather than symbolic.

Under these scheme monomials would look like this: (for example the term a11*b11 + a12*b21, that is the left top cell of the resulting matrix):

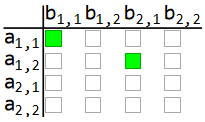
 In fact, here are all 4 bilinear terms that are sought to represent a matrix multiplication:

When we choose a bracket to expand, we, in fact, choose a subset of rows and columns in this representation and, after expansion, the entries corresponding to intersection of these rows and columns appear. There are the 8 multiplications that arrive from trivial application of matrix multiplication:

 These terms are enough to represent each of the 4 terms required in the answer.

Here is what Strassen proposes:

Here you can discover a new notation - red squares. Green square means a term is with +1 coefficient, white square means 0 coefficient and red square means -1 coefficient in front of the term.

Here is how Strassen proposes to take individual terms of his basis to produce resulting matrix (in this animation the top left square).

Pay close attention to "Sum" section and see how terms successively cancel:

 Where did Strassen take out these bases? As if out of thin air. Let's find them too.

 4. Brute force method

We live in a world of modern computers. Instead of struggling with ad hoc tricks, we can ask the machine to do the heavy lifting. Let's encode all monomials, define the target space, and instruct the computer to try every possible 7-element basis. Linear algebra over tells us whether a candidate spans the right space. Is it possible, what Strassen once discovered through intuition, can now be rediscovered mechanically in under an hour of compute time?

5. Strassen's Perspective, Modular First

The key insight is to treat the problem modulo 2 first. Why? Because the writer does not know how to solve the sign assignment problem in reasonable time. But whatever basis is selected, it sure better be solvable in modulo 2 arithmetic. That's how we will start. Once solvability mod 2 is established, if, some bases will be found, we can ask mathematical package (such as Wolfram Mathematica) to find the signs.

To make sure brute force works fast, usage of a modern low-level language such as C++ is proposed. The mod 2 matrix can be packed into a compact 16 bit representation.

The structure to represent such a matrix may look like this:

// Mod 2 matrix packed into 16 bit integer
struct mat {
	uint16_t pack = 0;  // 16 bits to store 4x4 matrix

	// Default constructor
	mat() = default;

	// Constructor from uint16_t
	explicit mat(uint16_t value) : pack(value) {}

	// Compute bit index from row (i) and column (j)
	constexpr int index(int i, int j) const { return i * 4 + j; }

	// Get the bit at (i,j)
	bool get(int i, int j) const {
		return (pack >> index(i, j)) & 1;
	}

	// Set the bit at (i,j) to 1
	void set(int i, int j) {
		pack |= (1 << index(i, j));
	}

	// Clear the bit at (i,j) to 0
	void clear(int i, int j) {
		pack &= ~(1 << index(i, j));
	}

	// Toggle the bit at (i,j)
	void toggle(int i, int j) {
		pack ^= (1 << index(i, j));
	}

	// Print as 4x4 matrix
	void print() const {
		for (int i = 0; i < 4; ++i) {
			for (int j = 0; j < 4; ++j) {
				std::cout << get(i, j) << " ";
			}
			std::cout << "\n";
		}
	}

	mat add(const mat& m) const {
		return mat(pack ^ m.pack);
	}

	// Comparison operators
	bool operator==(const mat& other) const { return pack == other.pack; }
	bool operator!=(const mat& other) const { return pack != other.pack; }
	bool operator<(const mat& other) const { return pack < other.pack; }
	bool operator<=(const mat& other) const { return pack <= other.pack; }
	bool operator>(const mat& other) const { return pack > other.pack; }
	bool operator>=(const mat& other) const { return pack >= other.pack; }
};

The main workhorse procedure will be the magical function that checks if selected basis can represent a sough term:

// Implements a linear independence–based solvability check for linear equations over the field F2
// using XOR Gaussian elimination in compressed form.
// The method is widely used in competitive programming for problems involving XOR combinations.
static bool check_solvability_over_gf2(
	const std::vector<uint16_t>& masks, uint16_t target)
{
	static std::vector<uint16_t> basis;
	basis.clear();
	for (uint16_t m : masks)
	{
		for (uint16_t b : basis)
			m = std::min(m, (uint16_t)(m ^ b));
		if (m > 0)
		{
			basis.push_back(m);
			std::sort(basis.rbegin(), basis.rend());
		}
	}
	for (uint16_t b : basis)
		target = std::min(target, (uint16_t)(target ^ b));
	return target == 0;
}

The procedure is so extremely fast and efficient, on this particular PC it can evaluate ~10^8 bases per second.

Having these procedures, we can now, albeit crudely, attempt to find some candidate bases:

for (int i1 = 0; i1 < mats.size(); ++i1) {
for (int i2 = i1 + 1; i2 < mats.size(); ++i2) {
for (int i3 = i2 + 1; i3 < mats.size(); ++i3) {
for (int i4 = i3 + 1; i4 < mats.size(); ++i4) {
for (int i5 = i4 + 1; i5 < mats.size(); ++i5) {
for (int i6 = i5 + 1; i6 < mats.size(); ++i6) {
for (int i7 = i6 + 1; i7 < mats.size(); ++i7) {
    evals++;
    if (evals % 100000000 == 0) {
        printf("%lld\n", evals);
    }

    basis = { mats[i1],mats[i2],mats[i3],mats[i4],mats[i5],mats[i6],mats[i7] };

    if (is_valid_basis(basis)) {
        printf("start");
        for (const auto& b : basis) {
            b.print();
        }
        printf("end");
    }
}
}
}
}
}
}
}

The full listing is available here (bilinear form enumeration and etc)

6. Sign assignment

The space of candidates is large. C(100,7) = 16007560800. A full search takes about 30 minutes on modern hardware. From all possibilities, 4 valid bases appear. They are:

Where x is either +1 or -1, which we have to determine. But how does one do that? We will use Wolfram Mathematica package to do so. Consider the first basis. Let's turn each x-entry into a product of chosen sign over row and column.

Here r[i,j] means that row j in i'th basis was chosen with r[i,j] sign (+1 or -1), and c[i,j] means that column j in i'th basis was chosen with c[i,j] sign (+1 or -1):

Each of these basis will individually be multiplied by x[i,j], meaning basis j goes into i'th result with sign x[i,j] (+1 or -1).

We equalize each cell of the sum to the cell we want to obtain in resulting monomial.

This produces 16*4=64 equations, and, after discarding spurious ones, 40 equations remain with 84 variables. Here is one of them:

c[1, 1] r[1, 1] x[1, 1] + c[3, 1] r[3, 1] x[1, 3] == 1

Wolfram Mathematica can easily supply us with sign assignment readily and without questions via the amazing NMinimize function:

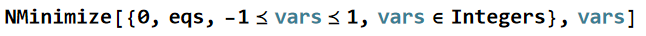
The complete Wolfram Mathematica Notebook solving the sign assignment can be found here

7. Conclusion

This method provides a systematic, reproducible derivation of Strassen’s formulas. No ad hoc guesses, no unexplained algebraic magic. Just a clean brute-force exploration guided by modular arithmetic. In principle, if someone were stranded on an island with only a computer and no memory of Strassen’s trick, this approach would allow them to reconstruct the scheme from scratch.

Additionally the method can be applied to minimize rank of any bilinear form, for example, like Karatsuba multiplication.

8. Addendum, Listing of all Found Bases

This one is Strassen's!